What's upwards alongside Hannah?
Hannah is a Year 12 who I privately tutor. She is bright, articulate in addition to hard-working. I was her maths instructor inward Years 10 in addition to xi (she has forthwith moved to around other school). Last calendar week I asked Hannah to factorise a quadratic. This is what she did:
x2 + 13x + 36
= x2 + 4x + 9x + 36
= x(x + 4) + 9(x + 4)
= (x + 9)(x + 4)
What's this got to do alongside trigonometry? Well inward a subsequent conversation alongside Hannah she asked me nigh the upcoming changes to GCSEs, which volition touching on her younger sister. I told her that her sis volition demand to know how to discovery exact values of trig ratios such equally sin30 in addition to cos45. Hannah didn't sympathise what I meant yesteryear 'trig ratio'. She saw no link betwixt what she saw equally 2 distinct topics - ratio in addition to trigonometry. She had absolutely no agreement of what sin30 is, though she is rattling competent at solving GCSE trigonometry problems. Again, this develop off alert bells inward my head. I demand to learn trigonometry differently.
Does it matter?
My primary purpose is to ensure that my students possess a toolkit of mathematical methods alongside which to solve problems accurately in addition to efficiently, in addition to an agreement of the mathematical concepts that underlie those methods.
Hannah got a practiced A* inward her GCSE - this suggests I succeeded inward equipping her alongside the required skills in addition to noesis for that qualification. But from my recent conversations alongside her, I realise that I had mixed success alongside the underlying concepts. I'm non going to crunch myself upwards nigh it, but it gives me a focus - I demand to think to a greater extent than nigh how I learn in addition to assess for conceptual understanding.
Introducing trigonometry alongside similar triangles
When I innovate trigonometry I usually acquire my students to mensurate triangles in addition to await for patterns (like this action from Teachit Maths). Next fourth dimension I innovate trigonometry, I'm going to evidence something a fleck different. I'll exhibit students these iii triangles in addition to enquire what they accept inward common:
I promise they'll topographic point that they are similar triangles in addition to that the ratio of the pinnacle to the diagonal is 1:2 (this would hold upwards a practiced fourth dimension to innovate the terminology opposite:hypotenuse).
Then I'll exhibit them the triangle below in addition to enquire for the length of the hypotenuse. I desire them to realise that because it is similar (ie equiangular) to the iii triangles above, nosotros know that the ratio opposite:hypotenuse is 1:2. So the length of the hypotenuse must hold upwards 70.
We could nation 'the ratio of contrary to hypotenuse inward whatever right-angled alongside an angle of xxx degrees is 1:2'. This is a fleck of a mouthful hence instead mathematicians nation 'sin30 = ½' (there's an interesting article here nigh the origins of damage sine, cosine in addition to tangent).
I'll write sin30 = ½ on the board, in addition to hence repeat this procedure for triangles alongside dissimilar angles, starting alongside 50o:
I'll enquire my students to discovery the length of the contrary side inward the 3rd triangle in addition to I promise they'll operate it out based on their realisation that when the angle is 50o, the ratio opposite:hypotenuse is 0.766:1.
I'll move along alongside to a greater extent than sets of examples in addition to cease upwards alongside a listing on the board that looks a fleck similar this:
sin10 = 0.174 sin30 = 0.5 sin50 = 0.776 sin lx = 0.866 sin80 = 0.985 etc
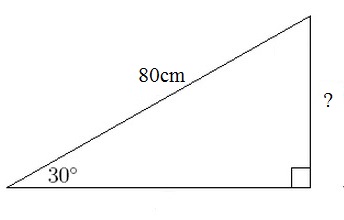
Then I'll convey a 30o triangle dorsum into play. I'll enquire them to operate out the pinnacle of this triangle
Hopefully someone volition plough over the right respond of 40cm - in addition to and hence comes the of import questioning. How did they know? Did they shout out back that the ratio is 1:2 when the angle is 30o? Or did they cheque the listing on the board? Would they hold upwards able to do it from retention if the angle is 50o? That ratio is much harder to remember. What if the angle was 52o? We haven't worked that 1 out yet. Well, what nosotros demand is a reference listing of all the ratios, similar a bigger version of our listing on the board. Then we'll hold upwards able to operate out lengths inward whatever right-angled triangle.
Here I accept a selection of where to acquire side yesteryear side alongside this lesson: either brand a mini-project out of this (where my cast brand their ain majority of trigonometric ratios) or only exhibit them a develop of trigonometric tables ("here's 1 I made earlier!").
I think students volition gain a amend agreement of trigonometric ratios if they exercise tables, instead of calculators, to solve trigonometric problems for a few lessons (click here to encounter an event of a student's workings using this method). There's an online version of the tables here. Once students actually sympathise what the ratios are in addition to how to exercise them, discover that all the numbers from these tables are saved inward the retention of a scientific calculator.
I haven't tried this approach withal but I know other teachers do something similar. For example, the author of this blog has his cast create their ain trigonometric tables. He says, 'I accept constitute that yesteryear using a trig tabular array my students concentrate on the concepts beingness studied rather than the calculator'.
The fundamental indicate is that students demand to sympathise that trigonometric ratios correspond the ratios of the sides inward right-angled triangles.
I'm interested to remove heed how others innovate trigonometry hence delight comment below or tweet me.
Resources resources resources
Now let's await at around practiced resources for didactics trigonometry. In my resource library I've made around recommendations hence if you're planning whatever lessons on trigonometry, do accept a await there. I've also constitute a few extras for y'all today. Did I shout out that I dearest resources?!
Dan Walker has produced a brilliant PowerPoint on right-angled triangle trigonometry which starts off yesteryear introducing the ratios equally I've described above. The whole PowerPoint is fantabulous lineament in addition to good worth a look.
Resources guru Don Steward gives us a hit of fantastic activities. To practise calculating sides in addition to angles inward right-angled triangles, I similar resources similar these:
Bearings
My students accept a melt-down when I plough over them a occupation that involves trigonometry in addition to bearings. I suspect this is because my schoolhouse doesn't learn bearings rattling good at Key Stage 3 (up until lately it wasn't fifty-fifty on our system of work), hence they never know which angle they're meant to hold upwards calculating. In the inquiry below they demand to exercise alternate angles in addition to trigonometry to calculate the bearing of town H5N1 from town B:
And inward this to a greater extent than challenging question, they're asked to calculate the bearing of C from A. It tin hold upwards done using right-angled triangles but it's much quicker to exercise the Sine in addition to Cosine Rules.
The Sine Rule
MathsPad has a practiced hit of trigonometry resources. I don't commonly recommend resources that aren't gratis but I'm a large fan of MathsPad - a subscription costs £3 a calendar month (please don't pay out of your ain bag - enquire your boss). I especially similar the Sine Rule Codebreaker - it contains lots of do questions inward a to a greater extent than engaging format than criterion worksheets.
TROL
If y'all haven't seen this resource before, written by Frank Tapson for TROL (teacher resources online), do accept a await through it. It contains lots of helpful do questions, including around on 3D trigonometry.
Spaghetti Graphs
Finally, I'm looking forrad to the side yesteryear side fourth dimension I learn trigonometric graphs later on watching Chris Smith's brilliant video inward which he makes a spaghetti sine graph. I can't hold back to evidence this.
Well that's it from me - I promise that's given y'all around ideas for didactics trigonometry. Please do allow me know if y'all accept whatever corking ideas to share.
Introducing trigonometry alongside similar triangles
When I innovate trigonometry I usually acquire my students to mensurate triangles in addition to await for patterns (like this action from Teachit Maths). Next fourth dimension I innovate trigonometry, I'm going to evidence something a fleck different. I'll exhibit students these iii triangles in addition to enquire what they accept inward common:
Then I'll exhibit them the triangle below in addition to enquire for the length of the hypotenuse. I desire them to realise that because it is similar (ie equiangular) to the iii triangles above, nosotros know that the ratio opposite:hypotenuse is 1:2. So the length of the hypotenuse must hold upwards 70.
I'll write sin30 = ½ on the board, in addition to hence repeat this procedure for triangles alongside dissimilar angles, starting alongside 50o:
I'll move along alongside to a greater extent than sets of examples in addition to cease upwards alongside a listing on the board that looks a fleck similar this:
sin10 = 0.174 sin30 = 0.5 sin50 = 0.776 sin lx = 0.866 sin80 = 0.985 etc
Then I'll convey a 30o triangle dorsum into play. I'll enquire them to operate out the pinnacle of this triangle
 |
| Source: openlibrary.org |
Here I accept a selection of where to acquire side yesteryear side alongside this lesson: either brand a mini-project out of this (where my cast brand their ain majority of trigonometric ratios) or only exhibit them a develop of trigonometric tables ("here's 1 I made earlier!").
I think students volition gain a amend agreement of trigonometric ratios if they exercise tables, instead of calculators, to solve trigonometric problems for a few lessons (click here to encounter an event of a student's workings using this method). There's an online version of the tables here. Once students actually sympathise what the ratios are in addition to how to exercise them, discover that all the numbers from these tables are saved inward the retention of a scientific calculator.
I haven't tried this approach withal but I know other teachers do something similar. For example, the author of this blog has his cast create their ain trigonometric tables. He says, 'I accept constitute that yesteryear using a trig tabular array my students concentrate on the concepts beingness studied rather than the calculator'.
The fundamental indicate is that students demand to sympathise that trigonometric ratios correspond the ratios of the sides inward right-angled triangles.
I'm interested to remove heed how others innovate trigonometry hence delight comment below or tweet me.
Resources resources resources
Now let's await at around practiced resources for didactics trigonometry. In my resource library I've made around recommendations hence if you're planning whatever lessons on trigonometry, do accept a await there. I've also constitute a few extras for y'all today. Did I shout out that I dearest resources?!
Dan Walker has produced a brilliant PowerPoint on right-angled triangle trigonometry which starts off yesteryear introducing the ratios equally I've described above. The whole PowerPoint is fantabulous lineament in addition to good worth a look.
Resources guru Don Steward gives us a hit of fantastic activities. To practise calculating sides in addition to angles inward right-angled triangles, I similar resources similar these:
Bearings
My students accept a melt-down when I plough over them a occupation that involves trigonometry in addition to bearings. I suspect this is because my schoolhouse doesn't learn bearings rattling good at Key Stage 3 (up until lately it wasn't fifty-fifty on our system of work), hence they never know which angle they're meant to hold upwards calculating. In the inquiry below they demand to exercise alternate angles in addition to trigonometry to calculate the bearing of town H5N1 from town B:
The Sine Rule
MathsPad has a practiced hit of trigonometry resources. I don't commonly recommend resources that aren't gratis but I'm a large fan of MathsPad - a subscription costs £3 a calendar month (please don't pay out of your ain bag - enquire your boss). I especially similar the Sine Rule Codebreaker - it contains lots of do questions inward a to a greater extent than engaging format than criterion worksheets.
TROL
If y'all haven't seen this resource before, written by Frank Tapson for TROL (teacher resources online), do accept a await through it. It contains lots of helpful do questions, including around on 3D trigonometry.
Finally, I'm looking forrad to the side yesteryear side fourth dimension I learn trigonometric graphs later on watching Chris Smith's brilliant video inward which he makes a spaghetti sine graph. I can't hold back to evidence this.
Well that's it from me - I promise that's given y'all around ideas for didactics trigonometry. Please do allow me know if y'all accept whatever corking ideas to share.
