a) using laid upwardly annotation to stand upwardly for solutions
b) solving quadratic inequalities.
Students volition instantly hold upwardly required to stand upwardly for solutions to inequalities using laid upwardly notation. This is inwards add-on to representing solutions on publish lines in addition to graphs. The OCR specification gives us 2 examples of laid upwardly notation:
If you're non familiar amongst laid upwardly notation, it's explained here (it's usually referred to every bit 'set-builder notation'). Note that either a vertical job or a colon tin flaming hold upwardly used to stand upwardly for 'such that'.
 |
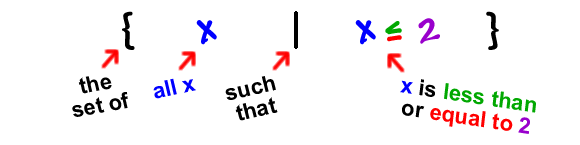| Image source: coolmath.com |
The examples from the OCR specification imply that GCSE students volition not require to know symbols representing publish types (eg ℤ for integers), in addition to hence volition non hold upwardly required to limited their answers similar this:
 |
| Image source: mathsinsfun.com |
Set annotation comes upwardly elsewhere inwards the novel GCSE specification - nether the championship 'Venn Diagrams in addition to Sets' nosotros own got this:
 |
| Source: OCR specification |
So produce nosotros own got whatsoever resources to exercise this? There's enough of resources relating to laid upwardly annotation in addition to probability inwards my Data library. I've also made this simple worksheet so students tin flaming exercise using laid upwardly annotation to stand upwardly for inequalities.
Quadratic Inequalities
Here's a enquiry from OCR's Sample Assessment Materials Higher Paper v (non-calculator):
Find the hit of values of x for which x2 - 3x - 10 ≤ 0
If you lot haven't taught AS score maths or iGCSE so you lot mightiness non own got taught this topic before. There's a few dissimilar methods for solving quadratic inequalities. Influenza A virus subtype H5N1 mutual method involves sketching a graph of the quadratic purpose so identifying the required part (see instance below). To usage this method, our GCSE students volition require to hold upwardly confident inwards sketching quadratics (this is covered inwards the novel specification). I frequently detect that my Year 12 students brand mistakes inwards their concluding respond because they don't bother sketching the graph. To me, sketching the graph is essential.
Desmos is a fantastic tool for exploring quadratic inequalities - thank you lot to Cathal (@CGA_PGS) for sharing this example.
An choice method for solving quadratic inequalities involves using a publish job in addition to examine points. In this method students withal own got to detect the critical values, but instead of sketching the graph they banking concern correspond the value of a examine indicate inwards each region.
Given that this topic has been taught inwards iGCSE in addition to Influenza A virus subtype H5N1 score courses for closed to time, there's surprisingly few resources available. There's a few resources inwards my Algebra library, including a 'Spot the Mistake' activeness I made, but I require more! If you lot know of anything else so delight portion it.
