H5N1 colleague asked me how I'd done it hence chop-chop in addition to I told her that I'd used divisibility rules. She said that she'd never taught divisibility rules because she'd never seen it specified on a system of work. It strikes me that this is a helpful chip of mathematical cognition that many secondary maths teachers don't teach. Do you lot instruct it? In what year? Most resources for this topic are aimed at psyche children but I intend nosotros should in all probability revisit it at Key Stage 3.
I was aware that my Year 10s didn't know the divisibility rules, hence I covered them every bit purpose of the 'Factors in addition to Multiples' topic this twelvemonth (ie with prime number factorisation, highest mutual ingredient etc). It's a skilful means to review the fundamentals of multiplication in addition to to railroad train fluency in addition to efficiency with numbers. To my Year 10s the rules seemed similar 'new' maths that they'd non seen earlier (or if they had, they couldn't retrieve it), hence it made an interesting in addition to suitably challenging lesson.
I also ran a session on divisibility rules with unopen to smart Year 3s in addition to 4s at a local psyche schoolhouse this year. They picked it upwards well, in addition to i time again I saw it every bit a skilful means to railroad train their agreement of multiplication in addition to their divulge fluency.
So it's a topic that industrial plant good with whatever historic menstruation group, from Key Stage 2 to Key Stage 4. Let's accept a quick await at the rules in addition to resources.
The Rules
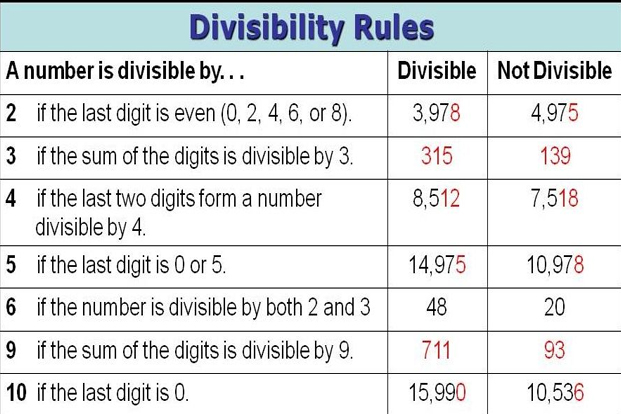
Most children volition easily hold out able to create upwards one's hear whether a divulge is divisible past times 2, five or 10. The neat 'tricks' are for 3 (the digit amount is divisible past times 3) in addition to ix (the digit amount is divisible past times 9). Once nosotros know whether a divulge divides past times 3, nosotros know whether it divides past times 6 (ie all even multiples of 3 are multiples of 6). For divisibility past times 4 at that spot are 2 alternatives: either banking corporation jibe whether the final 2 digits separate past times 4, or halve the divulge in addition to encounter if your respond is fifty-fifty (the 4 times tabular array existence double the 2 times table). The 7 key tests are shown inward the graphic below (there are loads of squeamish graphics for this on google images).
I didn't bother pedagogy the dominion for divisibility past times 7 because it's non straightforward. Rather in addition to hence memorise this dominion I idea my students would hold out ameliorate off but checking for divisibility past times 7 with long division.
If you're interested inward all the rules, from 1 - thirty in addition to beyond, banking corporation jibe out the Wikipedia page Divisibility rule.
Resources
I flora a mixture of uninspiring worksheets in addition to bizarre activities when I searched for resources online (the to a greater extent than odd activities included Divisibility Rock n' Rule, NFL divisibility dance and I'll take, you lot take...).
For the interactive whiteboard nosotros receive got Vectorkids: divisibility rules, Divisibility Test in addition to Delightfully Divisible.
If you're looking for a good structured worksheet pack, this is quite good.
This Don Steward.
Dan Walker has a keen laid upwards of slides in addition to activities on divisibility rules too, including this lovely Venn activity.
The ancient Greeks knew rules for divisibility past times 2, 3, five in addition to ix inward the 3rd century BC.
So why does the digit amount of multiples of 3 separate past times three? Sal Khan explains here...
He has a similar video for divisibility past times 9.
Do allow me know nearly your experiences of pedagogy divisibility rules in addition to whatever resources recommendations. If you've non taught it before, receive got a larn adjacent year. It's useful cognition in addition to good worth teaching.
